
Usually, the size and shape of the figure remain the same and only the direction gets opposite with the preimage. The point of reflection is said to be the mid-point where the reflection transformation takes place. The points on the surface of both the images are equidistant. Note that the point of reflection, in the case of origin reflection, changes the coordinates to a negative value, after the transformation of the shape.Ī reflection is a form of geometrical transformation, where the figure is flipped. By drawing a line segment at the point of reflection, you should note the line of origin, which is the figure’s mid-point. ‘Origin’ is the frequently used point.Īs you observed in the diagram above, the preimage triangle (original) has coordinates and the reflected image is.

What is the Reflection in the origin (0, 0)?Īny random area is used as the point of reflection in a coordinate plane. Note that the shape and size are left unchanged at the point of reflection. When you consider points over a figure, you will note exact points on the opposite direction of the original image, on the other side. Any structure is built using this reflection point as its single reference. The point of reflection is also referred to as the centre of a figure. Reflection of point is in the case of line Y = - X. Reflection of point is in the case of line Y = X. However, the signs get negated/cancelled when the point of reflection takes place over a line Y = - X, but the point of coordinates still changes places. Now, the X and Y coordinates will interchange their positions. Take the case where a point is reflecting across a line Y=X. Therefore, is the reflection of point and is changed as in the region of Y-Axis. Īs the contrary case of X-Axis, the Y-Axis here will stay the same while the X-coordinates transform with their opposite symbols when the reflection takes place across the Y-Axis. So, if the point of reflection is labelled as then the same coordinates across the X-Axis would be. Hence, the Y-coordinates will transform in their signs oppositely but the X-coordinates stay constant. Imagine that a point is reflecting over the X-Axis. The sub-headings followed down are details covered on reflection in the coordinate plane, with the X-Axis and Y-Axis as the references. Now, let us move onto the consideration of reflection with a graph. There is 1 line that helps in reflecting the object and this line is said to be the line of reflection.Īll About Reflection in the Coordinate Plane Since the position is changed in this transformation, there are chances for Translation as well.īoth the figures (before and after reflection) are equidistant from all their points over their surfaces.

However, the size and shape remain the same.
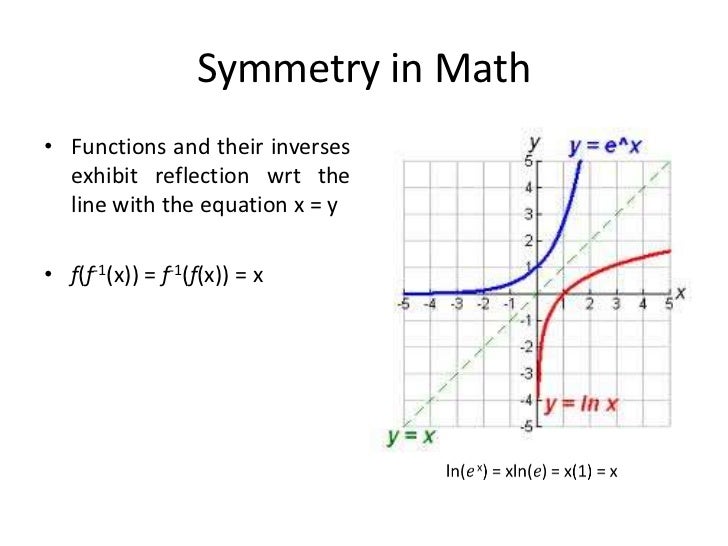
Only the direction of the resulting image is the opposite. So, the resulting image will be the mirror image to the origins structure. Now, let us learn the reflection definition by using the following pointers for a better understanding.įlipping an image is called a Reflection in geometry. We understood what a mathematical transformation. Important Points Regarding the ‘Reflection’ Definition Let’s take account of the 4th type Reflection and understand the highlighted concepts from the below sections. There are 4 major forms of transforming shapes namely, translation, rotation, dilation or resizing, and reflection. For example, when the length of a rectangle is reduced from 8 cm to 3 cm, then this is a form of geometrical transformation. In the same context, when we take mathematical transformation, this process is done to increase or decrease the size of an object or figure. Transformation is defined to be the process of changing something in its form, texture, shape, size, model, colour, etc.


 0 kommentar(er)
0 kommentar(er)
